 |
 |
||||||||||||||||||||||||||||||||||||||
|
Self-excited oscillations of collapsible tubes conveying fluids Self-excited oscillations of elastic tubes conveying fluid have been studied by numerous authors during last 30 years, generally in the context of various biological applications. Commonly used apparatus for experimental investigations of collapsible tubes have the principle scheme of “Starling resistor”. This scheme is also used in the apparatus of our laboratory. Note that the behavior of the tube as a part of such apparatus is independent problem, not directly applied to real physiological processes, and there are many works devoted to this apparatus.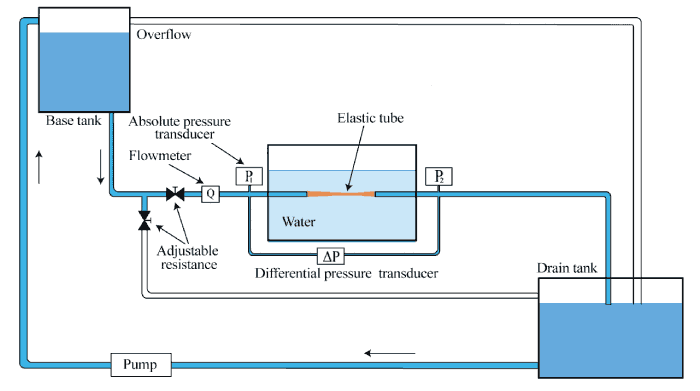
Experimental apparatus for investigations of stability and oscillations of elastic tubes conveying fluids.
Most experiments with elastic tubes conveying fluids are made in a wide range of the Reynolds numbers and often at turbulent flow regimes. However, bio-fluids mostly circulate at laminar regimes. The goal of experiments conducted in our laboratory is to compare the behavior of elastic tube conveying fluid at laminar and turbulent flow regimes. Typical experiment is as follows. We fix the flow rate Q by adjustable resistances, which defines the pressure at the tube inlet (upstream pressure p1). Then the pressure at the tube outlet (downstream pressure p2) is varied. The tube becomes unstable near its outlet end with the increasing of the pressure drop Δp=p1-p2. Types of occurred oscillations are shown in the movie.
Various regimes of oscillations of thin-walled elastic tube conveying water-glycerin mixture. The mixture flows from the right to the left. The outlet end of the tube is shown, where the pressure in the tube is minimum, and the oscillations are localised near this end.
Stability boundaries of the tube are obtained at various regimes. It is shown that they weakly depend on the fluid viscosity at both laminar and turbulent regimes. Limit cycle oscillations after the loss of stability and before single-frequency oscillations at fixed flow rate and increasing pressure drop is as follows. Two collapses of the tube are followed by a delay; for higher pressure drop three collapses are followed by a delay, and so on. At certain pressure drop, single-frequency oscillations occur and lock the tube. The influence of the pressure drop on the limit cycle is more significant at turbulent regimes. At laminar regimes for low flow rates the tube becomes collapsing with single frequency (i.e., with no delay) almost immediate after the loss of stability. 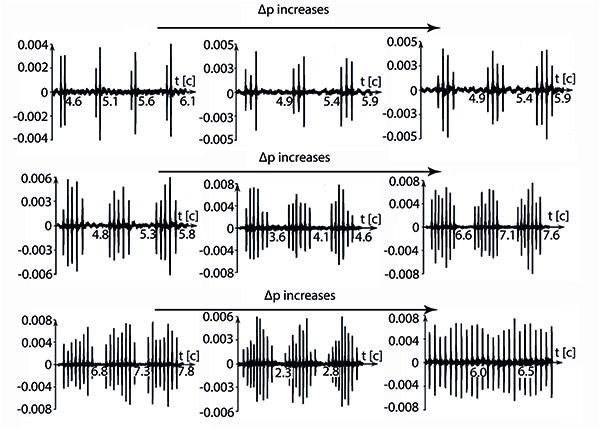
Limit cycle oscillations after the loss of stability and before single-frequency oscillations at fixed flow rate and increasing pressure drop. Microphone measurements.
The phenomenon known as “flow-rate limitation” is always observed after the loss of stability: the flow rate does not increase with further increase of the pressure drop. The main difference in the tube behavior at turbulent and laminar regimes is the amplitude of oscillations. It is always significantly higher at turbulent regimes. Also, frequency dependence on the pressure drop at the fixed flow rate is more pronounced at laminar than at turbulent regimes: the frequency grows faster with the pressure drop increase at laminar regimes. Next we are going to study the influence of non-Newtonian flows and fluid rheology on the elastic tubes stability. Theoretical line of investigations is related to the study of the flow stability of Newtonian and non-Newtonian nonlinear and visco-plastic fluids in circular tubes. A lot of theoretical results are obtained for Newtonian fluid, however, V.S. Yushutin showed that stability criteria for tubes with nonlinear fluid flows can significantly differ from the criteria for elastic tubes conveying Newtonian fluids. Now we theoretically and experimentally investigate flow stability in collapsible tubes with fluids of various non-Newtonian rheology. 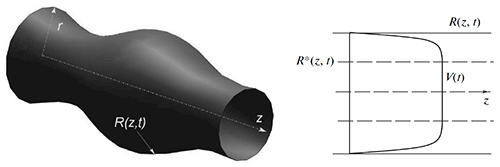
Axisymmetric deformation of the tube after the loss of stability (left). Longitudinal velocity profile for the visco-plastic fluid (right).
|
||||||||||||||||||||||||||||||||||||||
| Last update: june of 2025 | |||||||||||||||||||||||||||||||||||||||